Lo spazio colore CIEXYZ 1931

Il colore è una caratteristica degli oggetti basata puramente sulla nostra percezione. Se avessimo davanti a noi una foglia di una certa tonalità di verde, come potremmo descrivere a parole questo esatto colore a una persona che non la sta osservando? E se avessimo un ipotetico macchinario in grado di riprodurre tutti i colori possibili, quali istruzioni dovremmo dare per ricreare quella precisa sfumatura di verde? Sarebbero entrambe imprese impossibili.

Circa un secolo fa, qualche anno prima del 1930, si iniziò ad avvertire l'esigenza di trovare un modo per avere una descrizione precisa, univoca, dei colori, in modo che essi potessero essere identificati correttamente e replicati in modo fedele in caso di necessità. I risultati degli esperimenti condotti in quegli anni sono ancora oggi di estrema importanza, poiché costituiscono la base su cui sono costruite la rappresentazione e la gestione dei colori nel mondo digitale, nella  stampa a colori e in moltissimi altri settori dove la precisione cromatica è fondamentale.

In questo articolo, partendo da una descrizione semplificata del sistema visivo umano, vedremo come sono stati condotti quegli esperimenti e come grazie ad essi si sia arrivati a una rappresentazione matematica oggettiva dei colori.

Come è noto, la radiazione visibile costituisce una piccola parte dello spettro elettromagnetico. I nostri occhi possono percepire soltanto le lunghezze d'onda comprese nell'intervallo 380 - 750 nm (1 nanometro, nm, è pari a un miliardesimo di metro). Scendendo sotto i 380 nm troviamo nell'ordine (lunghezza d'onda via via decrescente) la radiazione ultravioletta, i raggi x e i raggi gamma, mentre oltre i 750 nm (lunghezza d'onda via via crescente) incontriamo la radiazione infrarossa, le microonde e le onde radio:

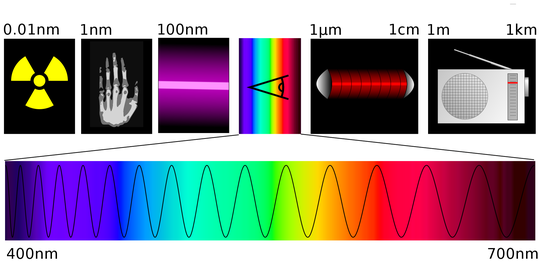
(Wikipedia - Tatoute and Phrood, CC BY-SA )

Il risultato percettivo del nostro sistema visivo alle lunghezze d'onda comprese nello spettro visibile è quello che noi chiamiamo colore. Esso altro non è che l'interpretazione del nostro cervello agli input provenienti dalla retina quando viene colpita dalle radiazioni dello spettro visibile. A ciascuna lunghezza d'onda tra 380 e 750 nm corrisponde un preciso colore spettrale, dal viola (380-435 nm) fino al rosso (625-750 nm). Nonostante lo spettro sia continuo, cioè non vi siano salti netti da un colore all'altro, si identificano solitamente sette intervalli corrispondenti ai colori

viola

indaco

blu

verde

giallo

arancione

rosso

Notiamo come in tutti i pannelli dedicati alla regolazione selettiva dei colori presenti nei software di post produzione, come il pannello HSL di Lightroom, sia intuitivamente mantenuto lo stesso ordine: 

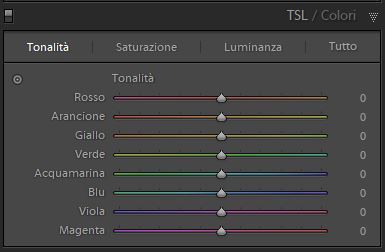
Un oggetto ci appare di un determinato colore perchè assorbe tutta la radiazione luminosa esclusa quella di una particolare lunghezza d'onda, che viene riflessa. Ad esempio un oggetto che riflette la radiazione luminosa con una lunghezza d'onda di 550 nm ci appare verde.

Quando osserviamo un oggetto, la luce passa attraverso la pupilla e raggiunge i fotorecettori sulla retina, dove viene convertita in segnali bioelettrici. Questi sono quindi inviati al cervello attraverso il nervo ottico.

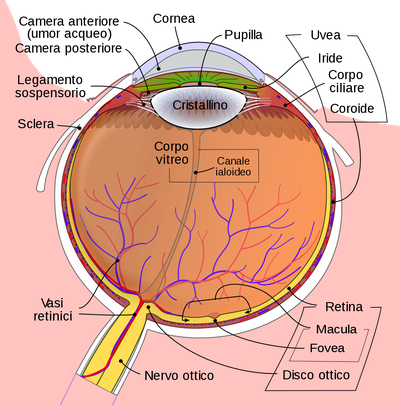
(Wikipedia -  derivative work B3t . And Jmarchn. / CC BY-SA)

Esistono due tipi di fotorecettori, i coni e i bastoncelli. I coni, concentrati nella zona centrale della retina (fovea), permettono la visione dei colori, in condizioni di buona luminosità (visione fotopica). I bastoncelli, concentrati nella zona periferica, servono invece per la visione al buio (visione scotopica), non sono in grado infatti di riconoscere i colori. Ai fini del tema che stiamo trattando ci concentreremo quindi sui coni.

Dalle prove sperimentali si è visto che le cellule coniche non presentano tutte la stessa sensibilità alla radiazione luminosa. Si possono distinguere tre tipologie di coni: alcuni percepiscono la luce con un picco di sensibilità nelle lunghezze d'onda più ampie (560-580 nm); altri presentano il picco nelle lunghezze d'onda medie (530-540 nm); altri ancora hanno il picco in corrispondenza delle lunghezze d'onda brevi (420-440 nm). Ciascun tipo è stato quindi contrassegnato con le lettere  L (long), M (medium) e S (short), per identificare la lunghezza d'onda a cui è più sensibile. Ma dato che queste lunghezze d'onda corrispondono nell'ordine ai colori rosso (red, R), verde (green, G) e blu (blue, B) i tre tipi di recettori vengono indicati talvolta anche con queste lettere. Nel grafico seguente sono riportate le curve di sensibilità normalizzate di questi tre tipi di coni alla radiazione visibile:

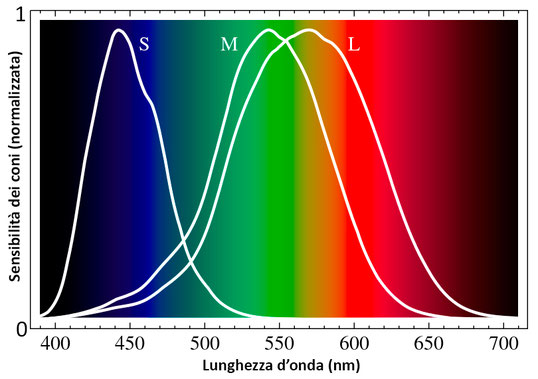
(Wikipedia)

E' stato anche osservato che la risposta allo stimolo luminoso da parte delle cellule coniche è sì proporzionale all'intensità della luce, ma solo entro certi limiti: un limite inferiore sotto il quale  il cono non è più sensibile, e un limite superiore (di saturazione) oltre il quale la risposta è la stessa.

La percezione cromatica di un determinato colore è data quindi dalla combinazione delle risposte dei tre tipi di cono. Analizzando la risposta globale dell'occhio alla luce, è stata tracciata un'altra curva, che mostra come esso presenti una sensibilità decisamente maggiore al colore verde:

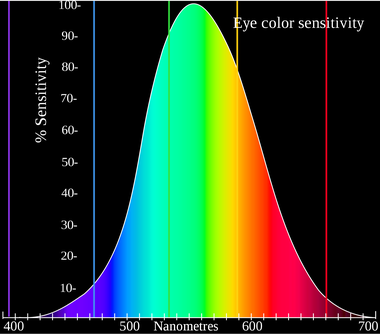
(Wikipedia - Skatebiker, vector by Adam Rędzikowski / CC BY-SA)

Se ci facciamo caso, noi siamo infatti in grado di distinguere molto bene le sfumature nei gialli e nei verdi, mentre ci è più difficile distinguerle nei rossi e ancora di più nei blu. Una ipotesi è che questo provenga da ragioni evolutive: per migliaia di anni l'uomo ha vissuto a contatto con la natura, dove i colori gialli e verdi prevalgono, e potrebbe avere sviluppato una maggiore sensibilità per la luce con queste lunghezze d'onda.

C'è un ultimo aspetto da considerare (il discorso è molto complesso ma non è di alcun interesse qui entrare troppo nel dettaglio): differenti distribuzioni spettrali possono generare la medesima risposta globale dell'insieme di coni, vale a dire la stessa sensazione cromatica. Questo fenomeno è detto metamerismo. Ad esempio, un oggetto che riflette solo il verde ci appare dello stesso colore di un oggetto che riflette le stesse quantità di blu e di giallo. Ogni colore può quindi essere creato da diverse distribuzioni spettrali purché determinino la stessa risposta da parte dei coni. Se partiamo dall'output, cioè dal colore che effettivamente percepiamo, non è possibile capire da quale distribuzione iniziale sia stato generato.

E' stato stimato che l'occhio umano sano sia in grado di percepire 8 milioni di differenti tonalità di colore. Questo numero come vedremo risulterà di un certo interesse quando parleremo degli spazi colore RGB e della profondità colore.

Verso la fine degli anni 20 del XX secolo W. David Wright e John Guild svolsero indipendentemente l'uno dall'altro alcune prove sperimentali con l'obiettivo di arrivare a una rappresentazione matematica, univoca, dei colori. Abbiamo visto che tutti i colori visibili dall'uomo sono individuati dall'elaborazione da parte del nostro cervello dei tre segnali corrispondenti ai livelli di stimolo dei tre tipi di coni (si parla infatti di tricromia). Gli esperimenti di Wright e Guild presero spunto proprio da questa caratteristica del sistema visivo umano per svolgere delle prove di corrispondenza colore (color matching).

Ai partecipanti veniva mostrato un colore spettrale puro di riferimento (quindi corrispondente a una precisa lunghezza d'onda) ed essi dovevano provare a riprodurre lo stesso identico colore facendo variare l'intensità di tre sorgenti luminose, aventi lunghezze d'onda corrispondenti al rosso (700 nm), al verde (546.1 nm) e al blu (435.8 nm). Il colore risultante, ottenuto quindi per sintesi additiva delle luci emesse da queste tre sorgenti, doveva essere percepito ai loro occhi come identico a quello di riferimento. Si registravano quindi i valori di luminosità risultanti (in candele/m2) delle tre sorgenti, vale a dire la quantità di rosso, verde e blu necessarie a riprodurre il colore di riferimento quando miscelati. Facendo variare la lunghezza d'onda della sorgente di riferimento lungo tutto lo spettro visibile, a passi di 10 nm, e ripetendo l'esperimento, si determinarono queste tre curve r, g, b, note come "Color Matching Functions" (funzioni di corrispondenza colore):

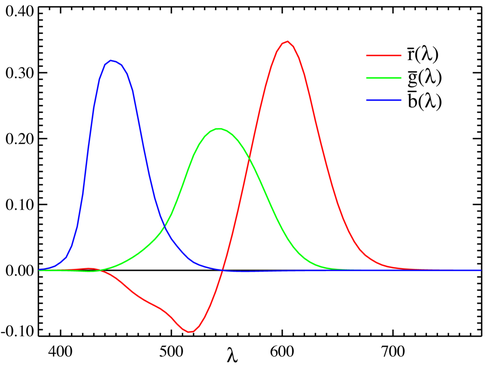
(Wikipedia)

Esse ci dicono quindi la quantità di rosso a 700 nm, di verde a 546.1 nm e di blu a 435.8 nm (chiamati colori primari) necessarie a riprodurre la luce a qualsiasi lunghezza d'onda. In realtà a queste funzioni si accompagnano anche alcune trasformazioni e dei fattori di scala per tenere conto del fatto che la sensibilità dell'occhio umano ai colori non è uniforme e altre ragioni più tecniche che tralasciamo. Si osservi che, come ci si aspettava, le funzioni r  e g sono nulle a 435.8 nm, r  e b  sono nulle a 546.1 nm e g  e b sono nulle a 700 nm. Il fatto che la curva del rosso presenti un valore molto piccolo in corrispondenza di 700 nm non deve trarre in inganno, è dovuto proprio ai fattori di scala citati. L'importante è aver capito che ogni radiazione monocromatica risulta quindi associata a tre numeri R, G, B (cioè i valori delle tre funzioni r, g, b alla lunghezza d'onda corrispondente), detti valori tristimolo, che rappresentano le luminosità delle tre sorgenti necessarie a ottenere il colore richiesto.

Di qui alla definizione di uno spazio tridimensionale il passo è breve. Ad esempio, preso l'arancione a 580 nm, possiamo individuare i valori R G B corrispondenti e riportarli in un sistema di coordinate tridimensionale dove gli assi rappresentano proprio i valori di R, G e B. Ripetendo l'operazione per tutte le lunghezze d'onda dello spettro visibile si va a tracciare nello spazio RGB una curva, che definisce quindi una rappresentazione matematica (tramite coordinate numeriche) di tutti i colori spettrali (spazio colore CIE RGB).

In realtà il riferimento RGB così ottenuto non fu poi utilizzato perchè le tre funzioni di corrispondenza dei colori che abbiamo visto presentano alcune problematiche. Molti potrebbero aver notato ad esempio che la curva r presenta dei valori negativi in un intervallo di lunghezze d'onda piuttosto ampio. Come è possibile? Questo significa che negli esperimenti Wright e Guild tutti i colori corrispondenti a questo intervallo non potevano essere ottenuti combinando i tre primari rosso, verde e blu, ma erano stati ottenuti aggiungendo il rosso alla sorgente luminosa di riferimento, invece che al verde e al blu Si pensi semplicemente a una equazione dove un termine negativo si può portare dall'altra parte dell'uguale cambiando il segno.

Per evitare questi problemi e in vista della definizione di uno standard, si decise di convertire, tramite una trasformazione lineare di coordinate, le curve r, g, b in nuove curve chiamate funzioni di corrispondenza colore x, y, z, che non presentano valori negativi. Il loro grafico è riportato qui sotto: 

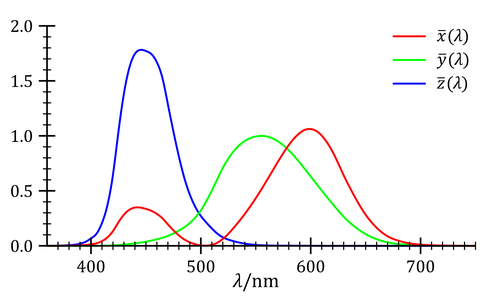
(Wikipedia - Acdx - CC BY-SA 4.0)

Questa trasformazione dalle le curve r g b alle nuove curve x y z ha in realtà un costo: i nuovi colori primari (che prima erano il rosso, il verde e il blu) ora non corrispondono più a colori reali, sono colori immaginari. Colori immaginari significa colori che è possibile definire matematicamente ma a cui non corrisponde una nostra sensazione visiva: sono "colori" ipersaturi estremamente chiari o estremamente scuri. Senza addentrarci troppo in questioni tecniche, si consideri che questo aspetto non costituisce in realtà un problema, avendo a disposizione le formule che mappano le curve x y z nelle curve originali r g b (formule oggi implementate nei software quindi automatizzate).

Dalle curve x y z si possono individuare i valori X, Y e Z corrispondenti a ciascuna lunghezza d'onda dello spettro visibile, esattamente come abbiamo visto per le curve r g b. Nel farlo furono adottate ulteriori accortezze matematiche:

- le coordinate X, Y, Z furono normalizzate, vale a dire trasformate in modo che potessero assumere valori da 0 a 1

- gli assi X, Y e Z furono scelti in modo da facilitare la rappresentazione grafica

- osservando che l'andamento della curva y  riprendeva fedelmente quello della  curva della sensibilità dell'occhio alla luce (le riporto qui sotto per un semplice confronto), si fece in modo che la curva y  fosse mappata in questa curva. Questo consentì di separare la cromaticità (quindi la tonalità e saturazione di un colore) dalla sua luminosità: la luminosità di un colore può così essere individuata dal solo valore della sorgente primaria corrispondente alla coordinata Y, mentre la sua cromaticità dipende solo dalle coordinate X e Z. 

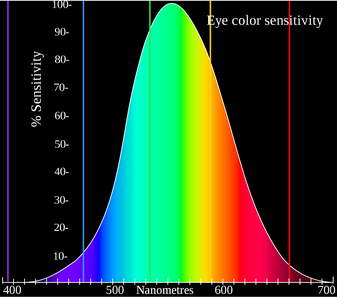
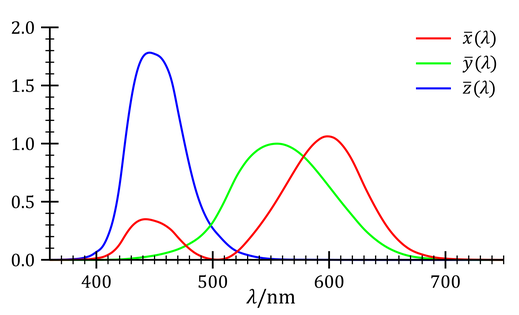
In definitiva, riportando nel riferimento XYZ la terna di coordinate X, Y, Z per tutte le radiazioni monocromatiche si ottiene la curva dei colori spettrali:

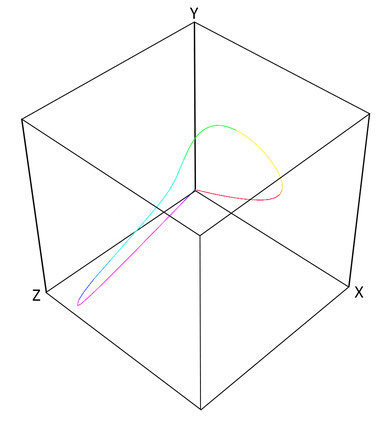
Tutti gli altri colori (vale a dire quelli non spettrali, non corrispondenti a una particolare lunghezza d'onda) si ottengono sommando vettorialmente due o più colori spettrali. Si arriva finalmente alla rappresentazione dello spazio colore CIEXYZ, adottato come standard nel 1931 dalla CIE (Commission Internationale de l'Eclarage - Commissione Internazionale sull'Illuminazione):

Esso comprende tutti i colori visibili dall'occhio umano medio, e a ciascuno è associata una terna di coordinate (X.Y,Z) che lo definisce in modo univoco. Il nero giace nell'origine degli assi, quindi nel punto di coordinate (0,0,0). A questo spazio colore si accompagna la definizione di Osservatore standard CIE 1931: in sostanza indica le condizioni di visione utilizzate durante le prove sperimentali di color matching, strettamente legate ai risultati ottenuti.

Una nota importante: come vedremo poco più avanti parlando degli spazi RGB, nessun monitor è in grado di riprodurre tutti i colori visibili dall'occhio umano! La gamma di colori che un display oggi può riprodurre (il suo gamut) è decisamente più piccola rispetto allo spazio XYZ. Qualsiasi rappresentazione visiva di questo spazio come quella qui sopra è di conseguenza soltanto una approssimazione ottenuta mappando i colori reali nei colori dello spazio sRGB (riproducibili da qualsiasi display).

L'importanza dello spazio CIEXYZ risiede nel fatto che esso è lo spazio di riferimento utilizzato per tutte le conversioni da altri spazi colore (in sostanza si tratta di trasformazioni di coordinate tramite prodotti matriciali). E' possibile a questo punto creare qualsiasi spazio colore adatto a soddisfare determinate esigenze pratiche (ad esempio vedremo più avanti alcuni spazi RGB) specificando le formule di trasformazione che lo legano allo spazio XYZ e sarà sempre possibile identificare correttamente i colori.